The applets in this section of Statistical Java allow you to see how levels of confidence are achieved through repeated sampling. The confidence intervals are related to the probability of successes in a Binomial experiment.

Contemporary Mathematics is designed to meet the scope and sequence requirements for a liberal arts mathematics course. This resource provides stand-alone sections with a focus on showing relevance in the features as well as the examples, exercises, and exposition. Contemporary Mathematics integrates technology applications, projects, and highlights a diverse group of contributors to mathematics, statistics, and related fields.

This is the first semester of a two-semester sequence on Differential Analysis. Topics include fundamental solutions for elliptic; hyperbolic and parabolic differential operators; method of characteristics; review of Lebesgue integration; distributions; fourier transform; homogeneous distributions; asymptotic methods.

Fall: Fundamental solutions for elliptic, hyperbolic and parabolic differential operators. Method of characteristics. Review of Lebesgue integration. Distributions. Fourier transform. Homogeneous distributions. Asymptotic methods. Spring: Sobolev spaces. Fredholm alternative. Variable coefficient elliptic, parabolic and hyperbolic linear partial differential equations. Variational methods. Viscosity solutions of fully nonlinear partial differential equations. The main goal of this course is to give the students a solid foundation in the theory of elliptic and parabolic linear partial differential equations. It is the second semester of a two-semester, graduate-level sequence on Differential Analysis.

Discrete Mathematics: An Open Introduction is a free, open source textbook appropriate for a first or second year undergraduate course for math majors, especially those who will go on to teach. The textbook has been developed while teaching the Discrete Mathematics course at the University of Northern Colorado. Primitive versions were used as the primary textbook for that course since Spring 2013, and have been used by other instructors as a free additional resource. Since then it has been used as the primary text for this course at UNC, as well as at other institutions.

Access also available here: http://discretetext.oscarlevin.com/home.php

Table of Contents
0 Introduction and Preliminaries 1

0.1 What is Discrete Mathematics?
0.2 Mathematical Statements
0.3 Sets
1 Counting

1.1 Additive and Multiplicative Principles
1.2 Binomial Coefficients
1.3 Combinations and Permutations
1.4 Combinatorial Proofs
1.5 Stars and Bars
1.6 Advanced Counting Using PIE
1.7 Chapter Summary
2 Sequences

2.1 Definitions
2.2 Arithmetic and Geometric Sequences
2.3 Polynomial Fitting
2.4 Solving Recurrence Relations
2.5 Induction
2.6 Chapter Summary
3 Symbolic Logic and Proofs

3.1 Propositional Logic
3.2 Proofs
3.3 Chapter Summary
4 Graph Theory

4.1 Definitions
4.2 Trees
4.3 Planar Graphs
4.4 Coloring
4.5 Euler Paths and Circuits
4.6 Matching in Bipartite Graphs
4.7 Chapter Summary
5 Additional Topics

5.1 Generating Functions
5.2 Introduction to Number Theory

Discrete Mathematics: An Open Introduction is a free, open source textbook appropriate for a first or second year undergraduate course for math majors, especially those who will go on to teach. The textbook has been developed while teaching the Discrete Mathematics course at the University of Northern Colorado. Primitive versions were used as the primary textbook for that course since Spring 2013, and have been used by other instructors as a free additional resource. Since then it has been used as the primary text for this course at UNC, as well as at other institutions.

Seminar on a selected topic from Renaissance architecture. Requires original research and presentation of a report. The aim of this course is to highlight some technical aspects of the classical tradition in architecture that have so far received only sporadic attention. It is well known that quantification has always been an essential component of classical design: proportional systems in particular have been keenly investigated. But the actual technical tools whereby quantitative precision was conceived, represented, transmitted, and implemented in pre-modern architecture remain mostly unexplored. By showing that a dialectical relationship between architectural theory and data-processing technologies was as crucial in the past as it is today, this course hopes to promote a more historically aware understanding of the current computer-induced transformations in architectural design.

Considers how institutions have been incorporated theoretically into explorations of growth and development. Four sets of institutions are examined in detail: the corporate sector, to study how ownership, strategy, and structure affect growth-related policies; financial institutions, to analyze how they condition savings and investment; labor market institutions, to investigate their impact on the determination of wage and production-related productivity; and the institutions associated with technology, such as universities, research laboratories, and corporate training centers, to consider how skill formulation is accomplished.

This book is not intended for budding mathematicians. It was created for a math program in which most of the students in upper-level math classes are planning to become secondary school teachers. For such students, conventional abstract algebra texts are practically incomprehensible, both in style and in content. Faced with this situation, we decided to create a book that our students could actually read for themselves. In this way we have been able to dedicate class time to problem-solving and personal interaction rather than rehashing the same material in lecture format.

Elementary Algebra is designed to meet the scope and sequence requirements of a one-semester elementary algebra course. The book’s organization makes it easy to adapt to a variety of course syllabi. The text expands on the fundamental concepts of algebra while addressing the needs of students with diverse backgrounds and learning styles. Each topic builds upon previously developed material to demonstrate the cohesiveness and structure of mathematics.

Table of Contents
1. Foundations
2. Solving Linear Equations and Inequalities
3. Math Models
4. Graphs
5. Systems of Linear Equations
6. Polynomials
7. Factoring
8. Rational Expressions and Equations
9. Roots and Radicals
10. Quadratic Equations

Access also available here: https://openstax.org/details/books/elementary-algebra

This text respects the traditional approaches to algebra pedagogy while enhancing it with the technology available today. In addition, textual notation is introduced as a means to communicate solutions electronically throughout the text. While it is important to obtain the skills to solve problems correctly, it is just as important to communicate those solutions with others effectively in the modern era of instant communications.While algebra is one of the most diversely applied subjects, students often find it to be one of the more difficult hurdles in their education. With this in mind, John wrote Elementary Algebra from the ground up in an open and modular format, allowing the instructor to modify it and leverage their individual expertise as a means to maximize the student experience and success. Elementary Algebra takes the best of the traditional, practice-driven algebra texts and combines it with modern amenities to influence learning, like online/inline video solutions, as well as, other media driven features that only a free online text can deliver.

Table of Contents
Chapter 1: Real Numbers and Their Operations
Chapter 2: Linear Equations and Inequalities
Chapter 3: Graphing Lines
Chapter 4: Solving Linear Systems
Chapter 5: Polynomials and Their Operations
Chapter 6: Factoring and Solving by Factoring
Chapter 7: Rational Expressions and Equations
Chapter 8: Radical Expressions and Equations
Chapter 9: Solving Quadratic Equations and Graphing Parabolas
Chapter 10: Appendix: Geometric Figures

Elementary Differential Equations with Boundary Value Problems is written for students in science, engineering, and mathematics who have completed calculus through partial differentiation. If your syllabus includes Chapter 10 (Linear Systems of Differential Equations), your students should have some preparation in linear algebra. In writing this book I have been guided by the these principles: An elementary text should be written so the student can read it with comprehension without too much pain. I have tried to put myself in the student's place, and have chosen to err on the side of too much detail rather than not enough. An elementary text can't be better than its exercises. This text includes 2041 numbered exercises, many with several parts. They range in difficulty from routine to very challenging. An elementary text should be written in an informal but mathematically accurate way, illustrated by appropriate graphics. I have tried to formulate mathematical concepts succinctly in language that students can understand. I have minimized the number of explicitly stated theorems and defonitions, preferring to deal with concepts in a more conversational way, copiously illustrated by 299 completely worked out examples. Where appropriate, concepts and results are depicted in 188 figures

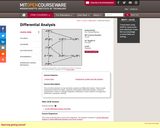
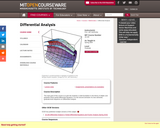
It is increasingly clear that the shapes of reality – whether of the natural world, or of the built environment – are in some profound sense mathematical. Therefore it would benefit students and educated adults to understand what makes mathematics itself ‘tick’, and to appreciate why its shapes, patterns and formulae provide us with precisely the language we need to make sense of the world around us. The second part of this challenge may require some specialist experience, but the authors of this book concentrate on the first part, and explore the extent to which elementary mathematics allows us all to understand something of the nature of mathematics from the inside.

The Essence of Mathematics consists of a sequence of 270 problems – with commentary and full solutions. The reader is assumed to have a reasonable grasp of school mathematics. More importantly, s/he should want to understand something of mathematics beyond the classroom, and be willing to engage with (and to reflect upon) challenging problems that highlight the essence of the discipline.

The book consists of six chapters of increasing sophistication (Mental Skills; Arithmetic; Word Problems; Algebra; Geometry; Infinity), with interleaved commentary. The content will appeal to students considering further study of mathematics at university, teachers of mathematics at age 14-18, and anyone who wants to see what this kind of elementary content has to tell us about how mathematics really works.

Table of Contents
I. Mental Skills

1.1 Mental arithmetic and algebra
1.2 Direct and inverse procedures
1.3 Structural arithmetic
1.4 Pythagoras' Theorem
1.5 Visualisation
1.6 Trigonometry and radians
1.7 Regular polygons and regular polyhedra
1.8 Chapter 1: Comments and solutions
II. Arithmetic

2.1 Place value and decimals: basic structure
2.2 Order and factors
2.3 Standard written algorithms
2.4 Divisibility tests
2.5 Sequences
2.6 Commutative, associative and distributive laws
2.7 Infinite decimal expansions
2.8 The binary numeral system
2.9 The Prime Number Theorem
2.10 Chapter 2: Comments and solutions
III. Word Problems

3.1 Twenty problems which embody "3 - 1 = 2"
3.2 Some classical examples
3.3 Speed and acceleration
3.4 Hidden connections
3.5 Chapter 3: Comments and solutions
IV. Algebra

4.1 Simultaneous linear equations and symmetry
4.2 Inequalities and modulus
4.3 Factors, roots, polynomials and surds
4.4 Complex numbers
4.5 Cubic equations
4.6 An extra
4.7 Chapter 4: Comments and solutions
V. Geometry

5.1 Comparing geometry and arithmetic
5.2 Euclidean geometry: a brief summary
5.3 Areas, lengths and angles
5.4 Regular and semi-regular tilings in the plane
5.5 Ruler and compasses constructions for regular polygons
5.6 Regular and semi-regular polyhedra
5.7 The Sine Rule and the Cosine Rule
5.8 Circular arcs and circular sectors
5.9 Convexity
5.10 Pythagoras' Theorem in three dimensions
5.11 Loci and coonic sections
5.12 Cubes in higher dimensions
5.13 Chapter 5: Comments and solutions
VI. Infinity: recursions, induction, infinite descent

6.1 Proof by mathematical induction I
6.2 'Mathematical induction' and 'scientific induction'
6.3 Proof by mathematical induction II
6.4 Infinite geometric series
6.5 Some classical inequalities
6.6 The harmonic series
6.7 Induction in geometry, combinatorics and number theory
6.8 Two problems
6.9 Infinite descent
6.10 Chapter 6: Comments and solutions

t is increasingly clear that the shapes of reality – whether of the natural world, or of the built environment – are in some profound sense mathematical. Therefore it would benefit students and educated adults to understand what makes mathematics itself ‘tick’, and to appreciate why its shapes, patterns and formulae provide us with precisely the language we need to make sense of the world around us. The second part of this challenge may require some specialist experience, but the authors of this book concentrate on the first part, and explore the extent to which elementary mathematics allows us all to understand something of the nature of mathematics from the inside.

The Essence of Mathematics consists of a sequence of 270 problems – with commentary and full solutions. The reader is assumed to have a reasonable grasp of school mathematics. More importantly, s/he should want to understand something of mathematics beyond the classroom, and be willing to engage with (and to reflect upon) challenging problems that highlight the essence of the discipline.

The book consists of six chapters of increasing sophistication (Mental Skills; Arithmetic; Word Problems; Algebra; Geometry; Infinity), with interleaved commentary. The content will appeal to students considering further study of mathematics at university, teachers of mathematics at age 14-18, and anyone who wants to see what this kind of elementary content has to tell us about how mathematics really works.

Continues 18.100. Roughly half the subject devoted to the theory of the Lebesgue integral with applications to probability, and half to Fourier series and Fourier integrals.

This open-source book by Crowell, Robbin, and Angenent is a spin-off of a previous open-source book by Robbin and Angenent. It covers the first semester of a freshman calculus course.

The basic principles of Einstein's general theory of relativity. Differential geometry. Experimental tests of general relativity. Black holes. Cosmology.

This book is designed for the transition course between calculus and differential equations and the upper division mathematics courses with an emphasis on proof and abstraction. The book has been used by the author and several other faculty at Southern Connecticut State University. There are nine chapters and more than enough material for a semester course. Student reviews are favorable.

It is written in an informal, conversational style with a large number of interesting examples and exercises, so that a student learns to write proofs while working on engaging problems.

This book is designed for the transition course between calculus and differential equations and the upper division mathematics courses with an emphasis on proof and abstraction. The book has been used by the author and several other faculty at Southern Connecticut State University. There are nine chapters and more than enough material for a semester course. Student reviews are favorable.

It is written in an informal, conversational style with a large number of interesting examples and exercises, so that a student learns to write proofs while working on engaging problems.

Access also available here: http://giam.southernct.edu/GIAM/

Table of Contents
Chapter 1: Introduction and notation
Chapter 2: Logic and quantifiers
Chapter 3: Proof techniques I
Chapter 4: Sets
Chapter 5: Proof techniques II -Induction
Chapter 6: Relations and functions
Chapter 7: Proof techniques III -Combinatorics
Chapter 8: Cardinality
Chapter 9: Proof techniques IV - Magic

Introduction to discrete and computational geometry. Topics covered: planar graphs, geometric graphs, the theory of crossings, extremal graph theory, arrangements of curves and points in the plane (mainly pseudolines and pseudocircles), problems involving distances, Gallai-Sylvester-type problems, Davenport-Schinzel sequences. Emphasis on teaching methods in combinatorial geometry. Many results presented are recent, and include open problems.